一、定义
1.1 感性解释
Bias和Variance是针对Generalization(泛化、一般化)来说的。在机器学习中,我们用训练数据集学习一个模型,我们通常会定义一个损失函数(Loss Function),然后将这个Loss(或者叫error)的最小化过程,来提高模型的性能(performance)。然而我们学习一个模型的目的是为了解决实际的问题(即将训练出来的模型运用于预测集),单纯地将训练数据集的Loss最小化,并不能保证解决更一般的问题时模型仍然是最优的,甚至不能保证模型是可用的。这个训练数据集的Loss与一般化的数据集(预测数据集)的Loss之间的差异就叫做Generalization error。
而Generalization error又可以细分为Random Error、Bias和Variance三个部分。
首先需要说的是随机误差。它是数据本身的噪声带来的,这种误差是不可避免的。其次如果我们能够获得所有可能的数据集合,并在这个数据集合上将Loss最小化,这样学习到的模型就可以称之为“真实模型”,当然,我们是无论如何都不能获得并训练所有可能的数据的,所以真实模型一定存在,但无法获得,我们的最终目标就是去学习一个模型使其更加接近这个真实模型。
Bias和Variance分别从两个方面来描述了我们学习到的模型与真实模型之间的差距(除去随机误差)。
Bias描述的是对于测试数据集,“用所有可能的训练数据集训练出的所有模型的输出预测结果的期望”与“真实模型”的输出值(样本真实结果)之间的差异。简单讲,就是在样本上拟合的好不好。要想在bias上表现好,low bias,就是复杂化模型,增加模型的参数,但这样容易过拟合 (overfitting)。
Variance则是“不同的训练数据集训练出的模型”的输出值之间的差异。
在一个实际系统中,Bias与Variance往往是不能兼得的。如果要降低模型的Bias,就一定程度上会提高模型的Variance,反之亦然。造成这种现象的根本原因是,我们总是希望试图用有限训练样本去估计无限的真实数据。当我们更加相信这些数据的真实性,而忽视对模型的先验知识,就会尽量保证模型在训练样本上的准确度,这样可以减少模型的Bias。但是,这样学习到的模型,很可能会失去一定的泛化能力,从而造成过拟合,降低模型在真实数据上的表现,增加模型的不确定性。相反,如果更加相信我们对于模型的先验知识,在学习模型的过程中对模型增加更多的限制,就可以降低模型的variance,提高模型的稳定性,但也会使模型的Bias增大。Bias与Variance两者之间的trade-off是机器学习的基本主题之一,机会可以在各种机器模型中发现它的影子。
1.2 图示解释
下图将机器学习任务描述为一个打靶的活动:根据相同算法、不同训练数据集训练出的模型,对同一个样本进行预测;每个模型作出的预测相当于是一次打靶。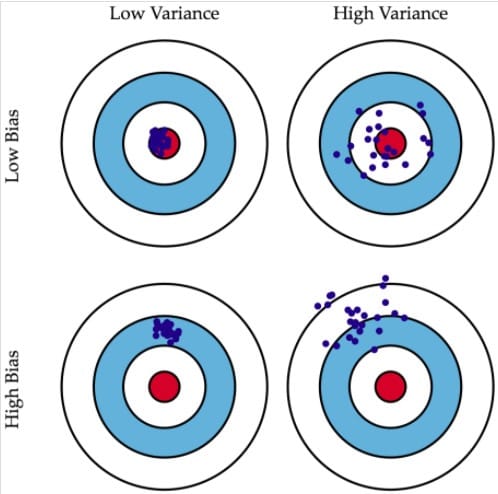
左上角的示例是理想状况:偏差和方差都非常小。如果有无穷的训练数据,以及完美的模型算法,我们是有办法达成这样的情况的。然而,现实中的工程问题,通常数据量是有限的,而模型也是不完美的。因此,这只是一个理想状况。
右上角的示例表示偏差小而方差大。靶纸上的落点都集中分布在红心周围,它们的期望落在红心之内,因此偏差较小。另一方面,落点虽然集中在红心周围,但是比较分散,这是方差大的表现。
左下角的示例表示偏差大而方差小。显而易见,靶纸上的落点非常集中,说明方差小。但是落点集中的位置距离红心很远,这是偏差大的表现。
右下角的示例则是最糟糕的情况,偏差和方差都非常大。这是我们最不希望看到的结果。
再看一个来自PRML的例子: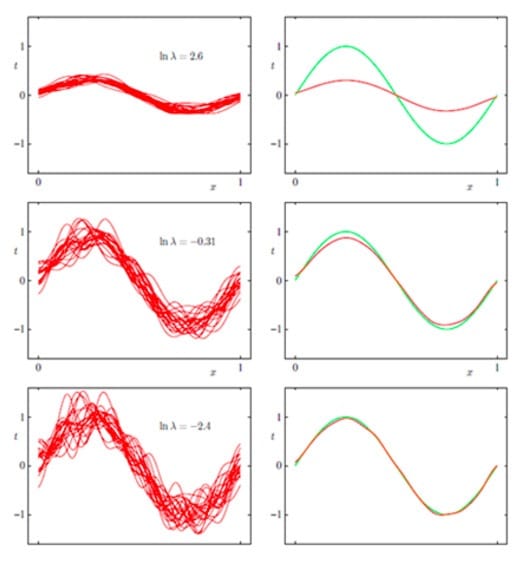
这是一个曲线拟合的问题,对同分布的不同数据集进行了多次的曲线拟合,左边表示方差(variance),右边表示偏差(bias),绿色是真实值函数。$In \lambda$表示的是模型的复杂度,这个值越小,表示模型的复杂程度越高,在第一行,大家的复杂度都很低的时候,方差是很小的,但是偏差很大;但是到了最后一幅图,我们可以得到,每个人的复杂程度都很高的情况下,不同的函数就有着天壤之别了,所以方差就很大,但此时偏差就很小了。
1.3 数学解释
排除人为的失误,人们一般会遇到三种误差来源:随机误差、偏差和方差。
首先需要说明的是随机误差。随机误差是数据本身的噪声带来的,这种误差是不可避免的。一般认为随机误差服从高斯分布,记作$\varepsilon ~N\left(0,\sigma_{\varepsilon}\right)$。因此,若有变量$y$作为预测值,以及$X$作为自变量(协变量),那么我们将数据背后的真实规律$f$记作
偏差和方差则需要在统计上做对应的定义。
- 偏差(Bias)描述的是通过学习拟合出来的结果的期望,与真实结果之间的差距,记作
- 方差(Variance)即为统计学中的定义,描述的是通过学习拟合出来的结果自身的不稳定性,记作
以均方误差为例,有如下推论:
二、如何Tradeoff
2.1 最佳平衡点
假设我们现在有一组训练数据,需要训练一个模型(基于梯度的学习)。在训练的起始,Bias很大,因为我们的模型还没有来得及开始学习,也就是与“真实模型”差距很大。然而此时variance却很小,因为训练数据集(training data)还没有来得及对模型产生影响,所以此时将模型应用于“不同的”训练数据集也不会有太大的差异。
而随着训练过程的进行,Bias变小了,因为我们的模型变得“聪明”了,懂得了更多关于“真实模型”的信息,输出值与真实值之间更加接近了。但是如果我们训练得太久了,variance就会变得很大,因为我们除了学习到关于真实模型的信息,还学到了许多具体的,只针对我们使用的训练集(真实数据的子集)的信息。而不同的可能的训练数据集(真实数据的子集)之间的某些特征和噪声是不一致的,这就导致了了我们在很多其他的数据集上就无法获得很好地效果,也就是所谓的Overfitting(过拟合)。
考虑到模型误差是偏差与方差的加和,因此我们可以绘制出这样的图像。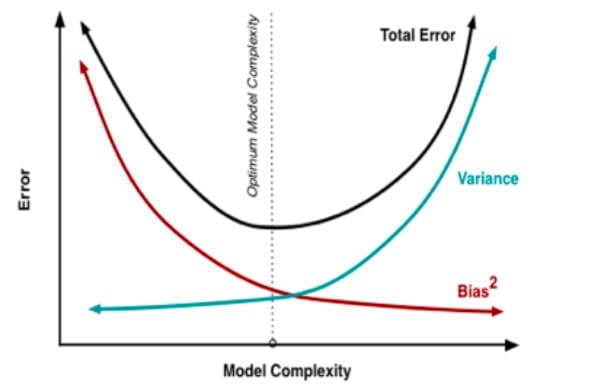
图中的最优位置,实际上是Total Error曲线的拐点。我们知道,连续函数的拐点意味着此处一阶导数的值为0。即
这个公式给出了寻找最优平衡点的数学描述。若模型复杂度小于平衡点,则模型的偏差会偏高,模型倾向于欠拟合;若模型复杂度大于平衡点,则模型的方差会偏高,模型倾向于过拟合。
3.2 过拟合与欠拟合的外在表现
尽管有了上述的数学表述,但是在现实环境中,有时候我们很难计算模型的偏差与方差。因此,我们需要通过外在表现,判断模型的拟合状态:是欠拟合还是过拟合。
同样地,在有限的训练数据集中,不断增加模型的复杂度,意味着模型会尽可能多地降低在训练集上的误差。因此在训练集上,不断地增加模型的复杂度,训练集上的误差会一直下降。
我们把数据分为三个部分:训练数据集、验证数据集、测试数据集。
因此,我们可以绘制出这样的图像。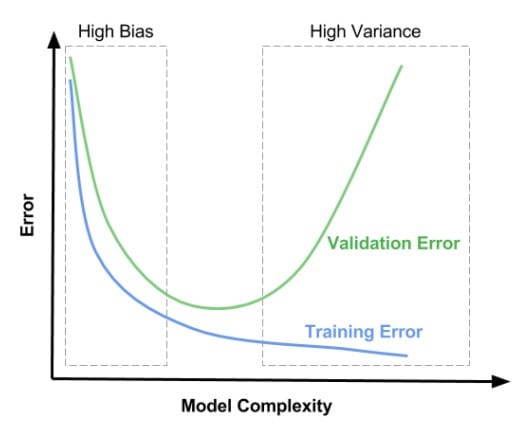
在上图左边区域,训练集与验证集的误差都很高,这块区域的偏差比较高。在右边区域,在验证集上误差很高,但是在训练集上偏差很低,这块区域的方差比较高。我们希望在中间的区域得到一个最优平衡点。
所以,偏差较高(欠拟合)有以下两个特征:
- 1)训练集误差很高
- 2)验证集误差和训练集误差差不多大
方差较高(过拟合)
- 1)训练集误差较低
- 2)非常高的验证集误差
3.3 如何处理欠拟合与过拟合
有了以上的分析,我们就能比较容易地判断模型所处的拟合状态。接下来,我们可以参考Ng提供的处理模型欠拟合与过拟合的一般方法了。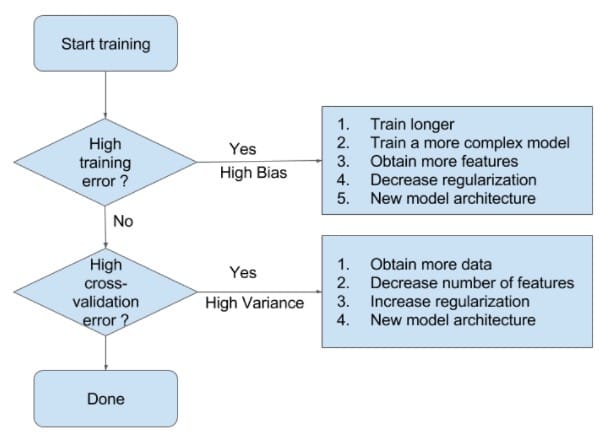
当模型处于欠拟合状态时,根本的办法是增加模型的复杂度。我们一般有以下一些办法:
- 1)增加模型迭代次数;
- 2)训练一个复杂度更高的模型:比如在神经网络中增加神经网络层数、在SVM中用非线性SVM(核技术)代替线性SVM
- 3)获取更多的特征以供训练使用:特征少,对模型信息的刻画就不足够了
- 4)降低正则化权重:正则化正是为了限制模型的灵活度(复杂度)而设定的,降低其权值可以在模型训练中增加模型复杂度。
当模型处于过拟合状态时,根本的办法是降低模型的复杂度。我们一般有以下一些办法:
- 1)获取更多的数据:训练数据集和验证数据集是随机选取的,它们有不同的特征,以致在验证数据集上误差很高。更多的数据可以减小这种随机性的影响。
- 2)减少特征数量
- 3)增加正则化权重:方差很高时,模型对训练集的拟合很好。实际上,模型很有可能拟合了训练数据集的噪声,拿到验证集上拟合效果就不好了。我们可以增加正则化权重,减小模型的复杂度。

